Shift space

In symbolic dynamics and related branches of mathematics, a shift space or subshift is a set of infinite words that represent the evolution of a discrete system. In fact, shift spaces and symbolic dynamical systems are often considered synonyms.

1 Notation
2 Definition
3 Characterization and sofic subshifts
4 Examples
5 Further reading
6 References

Notation

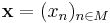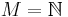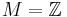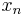Let A be a finite set of states. An infinite (respectively bi-infinite) word over A is a sequence $\mathbf x=(x_n)_{n\in M}$ , where $M=\mathbb N$ (resp. $M=\mathbb Z$ ) and $x_n$ is in A for any integer n. The shift operator $\sigma$ acts on an infinite or bi-infinite word by shifting all symbols to the left, i.e.,

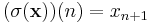$(\sigma(\mathbf x))(n)=x_{n%2B1}$ for all n.

In the following we choose 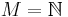$M=\mathbb N$ and thus speak of infinite words, but all definitions are naturally generalizable to the bi-infinite case.

Definition

A set of infinite words over A is a shift space if it is closed with respect to the natural product topology of 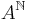$A^\mathbb N$ and invariant under the shift operator. Thus a set 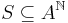$S\subseteq A^\mathbb N$ is a subshift if and only if

for any (pointwise) convergent sequence 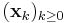$(\mathbf x_k)_{k\geq 0}$ of elements of S, the limit 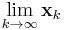$\lim_{k\to\infty}\mathbf x_k$ also belongs to S; and
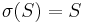$\sigma(S)=S$ .

A shift space S is sometimes denoted as 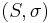$(S,\sigma)$ to emphasize the role of the shift operator.

Some authors^[1] use the term subshift for a set of infinite words that is just invariant under the shift, and reserve the term shift space for those that are also closed.

Characterization and sofic subshifts

A subset S of 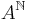$A^\mathbb N$ is a shift space if and only if there exists a set X of finite words such that S coincides with the set of all infinite words over A having no factor in X.

When X is a regular language, the corresponding subshift is called sofic. In particular, if X is finite then S is called a subshift of finite type.

Examples

The first trivial example of shift space (of finite type) is the full shift 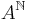$A^\mathbb N$ .

Let 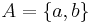$A=\{a,b\}$ . The set of all infinite words over A containing at most one b is a sofic subshift, not of finite type.

References

^ Thomsen, K. (2004). "On the structure of a sofic shift space" (PDF Reprint). Transactions of the American Mathematical Society 356 (9): 3557–3619. doi:10.1090/S0002-9947-04-03437-3. http://www.imf.au.dk/publications/pp/2003/imf-pp-2003-6.pdf. Retrieved 2008-01-29.